2D Linear Elasticity via PINN
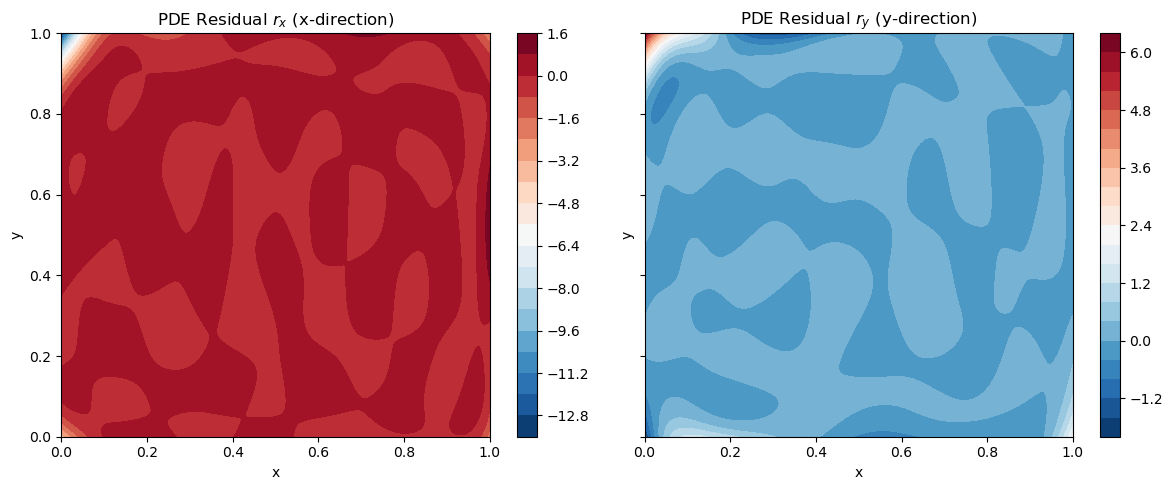
Obeyance of Navier-Cauchy equation by the PINN model for the collocation points
PINN, TensorFlow
Hypercube Sampling, 2D linear-elasticity
Lowest loss: 2.22 (6 layers, 15 neurons each)
What: Physics-informed NN for predicting the 2D linear elasticity parameters (Displacement, Shear-stress, BCs, laws) of an 1 sq. meter steel plate fixed at bottom under 4 Newton uniform vertical load.
Why: Reduce reliance on dense FEM labels and deliver fast, physics-consistent field predictions for design sweeps.
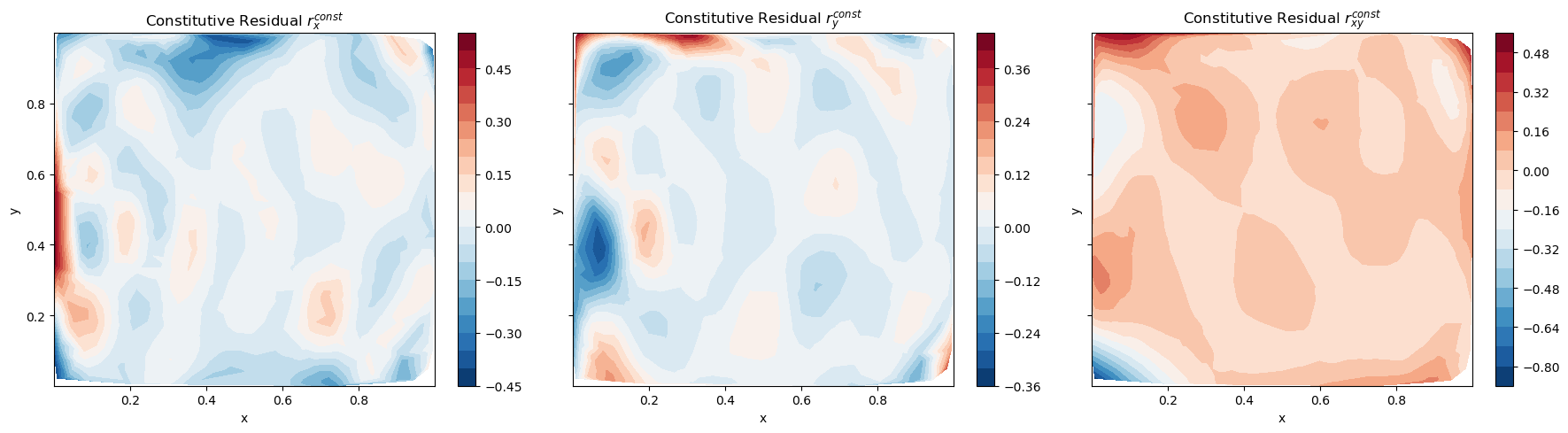
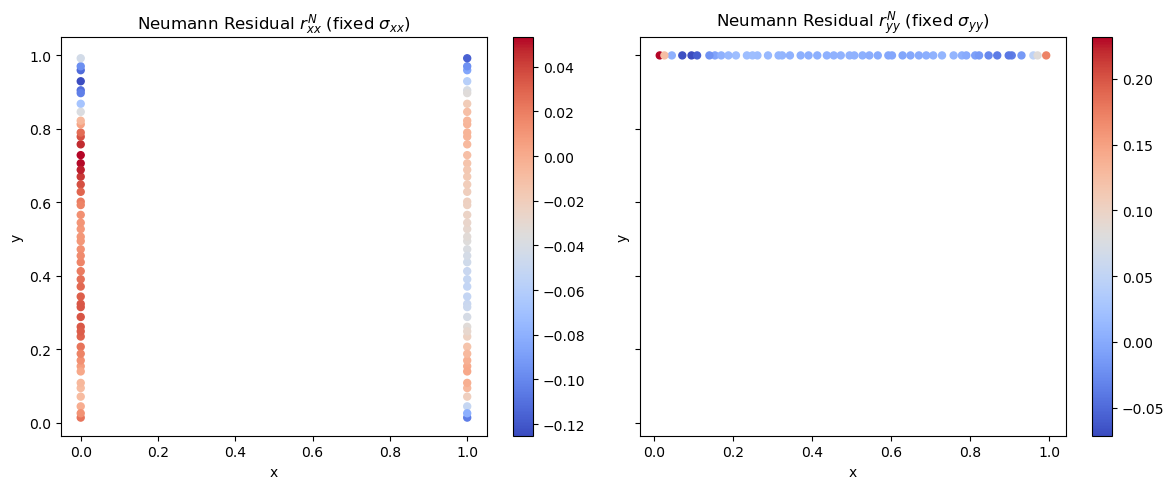
How: TensorFlow PINN with Navier–Cauchy + Hooke residuals; Latin-hypercube sampling of collocation (1k inside, 50 each boundary) points; Dirichlet/Neumann BCs; 27-config hyperparameter sweep with validation tracking.
Results: Best topology 6×15, dropout 0.3 (Glorot) reached val loss 2.22, producing smooth, physically coherent fields and a clear path to add R² vs FEM ground truth.